* 공부 목표
DP - 1463, 11726, 11727, 9095, 10844, 11057, 2193, 9465, 2156, 11053, 11055, 11722, 11054, 1912, 2579, 1699, 2133, 9461, 2225, 2011, 11052
문) 2행 n열로 배치된 스티커, 각 스티커마다 점수가 있음. 뗄 수 있는 스티커 합의 최대를 구하라. 단, 한 스티커를 떼면 주변에 붙어있는 스티커들은 망가져 사용할 수 없다.
입) 첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 두 줄에는 n개의 정수가 주어지며, 각 정수는 그 위치에 해당하는 스티커의 점수이다. 연속하는 두 정수 사이에는 빈 칸이 하나 있다. 점수는 0보다 크거나 같고, 100보다 작거나 같은 정수이다.
풀이
1. 테이블 정의
- 2*n열의 테이블, 각 2차원 배열에 해당하는 값도 입력받음
- 점수 합이 최댓값이면서 서로 변을 공유하지 않는 스티커 집합
2. 점화식 정의
- D[0][j] = Math.max(D[1][j-1], D[1][j-2]) + D[0][j]
- D[1][j] = Math.max(D[0][j-1], D[0][j-2]) + D[1][j]
이 점화식을 이해하는데 시간이 오래 걸렸다.
간단히 이야기하면
1) 입력 받은 sticker의 점수 배열
2) dp 배열을 구분하여
▶ dp배열에 sticker 점수 누적을 시키는 것이다.
그러면 점수 누적하는 방법이 중요하고, 그게 바로 이 문제의 핵인 점화식이 될 것이다.
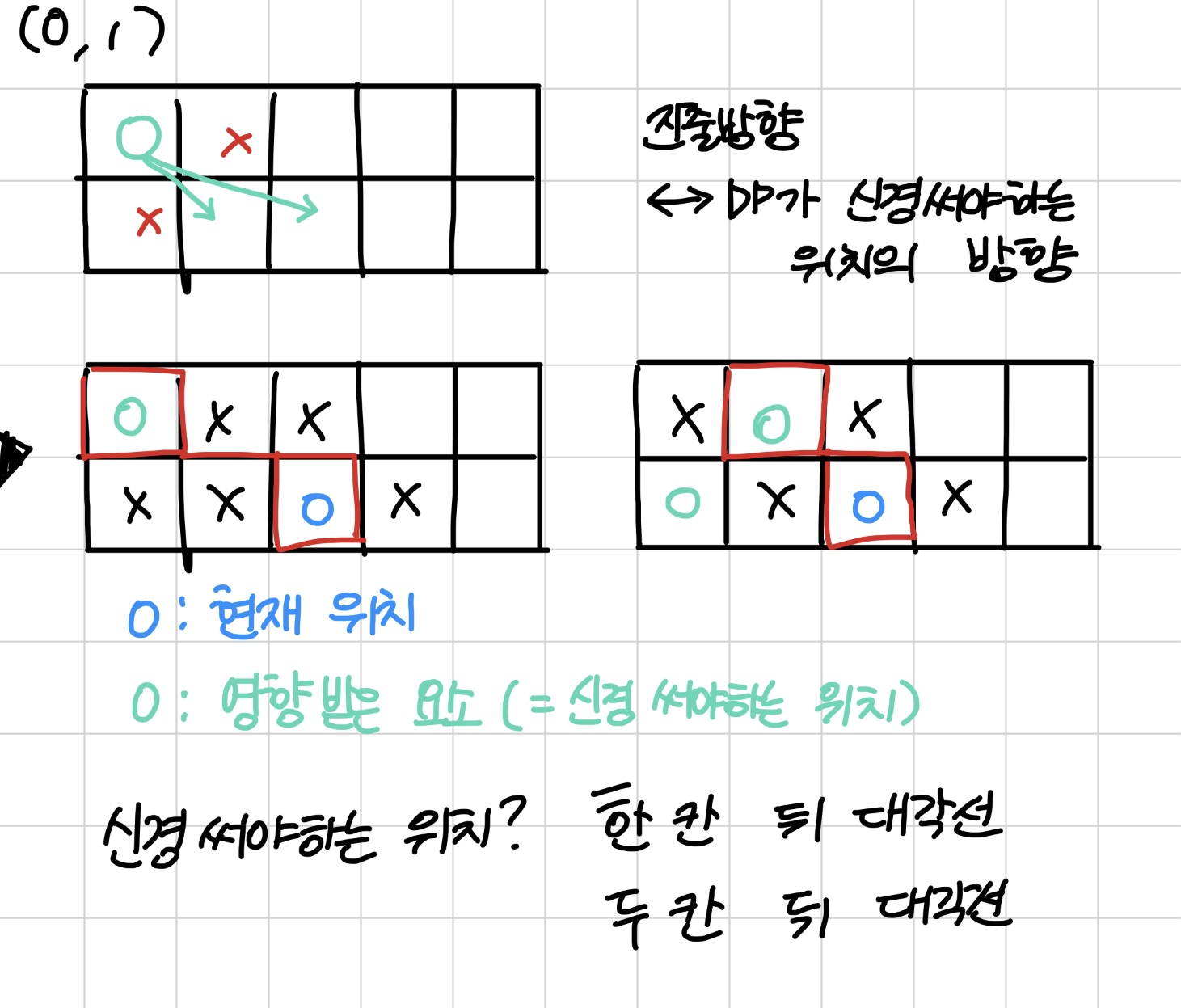
현재 위치에 영향 주는 건, 이전 항목이다.
이전 항목이 될 수 있는 건 <한 칸 뒤> 혹은 <두 칸 뒤> 대각선에 있던 항목이다.
현재 위치 = 현재 위치 값 + 이전 값 중 더 큰 값
- D[0][j] = Math.max(D[1][j-1], D[1][j-2]) + D[0][j]
고로 이런 점화식이 나오게 된다.
3. 초기값 정의
- D[0][1] = D[0][1]
- D[1][1] = D[1][1]
n=1일 때, D[0][1] 그리고 D[1][1]은 선택할 수 있는 최댓값이 자기 자신 밖에 없다.
코드
import java.util.Scanner;
public class num_9465 {
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt(); //반복 횟수
for(int k=0; k<T; k++) {
int n = sc.nextInt(); //열 갯수
int d[][] = new int[2][n+1];
int sticker[][] = new int[2][n+1];
//2차원 배열 채워넣기
for(int i=0; i<2; i++) {
for(int j=1; j<n+1; j++) {
sticker[i][j] = sc.nextInt();
}
}
//초기값
d[0][1] = sticker[0][1];
d[1][1] = sticker[1][1];
for(int j=2; j<n+1; j++) {
d[0][j]=Math.max(d[1][j-1], d[1][j-2]) + sticker[0][j];
d[1][j]=Math.max(d[0][j-1], d[0][j-2]) + sticker[1][j];
}
System.out.println(Math.max(d[0][n], d[1][n]));
}
sc.close();
}
}
** 잠깐! 열 값이 시작이 2인 이유?
(이건 뇌피셜 설명이고, 정확하지 않으니 참고만 해주세요)
1열 이상부터 시작하는 이유는, -1 index 오류가 나기 때문이고
2열 이상부터 시작하는 이유는, 1열에 해당하는 초기값은 정의되어있기 때문.
처음 문제를 보고 <안 되는 경우의 수>를 생각했다.
가령 코너 4개는 안 되는 게 2개고,
나머지는 좌우 위 또는 아래 이렇게 3개라는... 사실상 전혀 풀이에 도움 안 되는 생각 말이다.
DP의 본질에 집중하고,
순차적으로 진행해나가는 코드를 생각하는 것이 필요하다고 느꼈다.
'알고리즘' 카테고리의 다른 글
| [백준] DP - 2156번, 포도주 시식 (다른 풀이 봄) (0) | 2023.10.03 |
|---|---|
| [백준] 스택 - 28278번, 스택2 (0) | 2023.10.01 |
| [백준] DP - 2193번, 이친수 (0) | 2023.09.23 |
| [백준] DP - 10844번, 쉬운 계단 수 (답지 봄) (0) | 2023.09.22 |
| [백준] DP - 9095번, 1, 2, 3 더하기 (0) | 2023.06.22 |
