[백준] 정렬 - 11004번, k번째 수 (quicksort로 풀 수 있을까?)
문) 수 N개 A1, A2, ..., AN이 주어진다. A를 오름차순 정렬했을 때, 앞에서부터 K번째 있는 수를 구하는 프로그램을 작성하시오.
입) 첫째 줄에 N(1 ≤ N ≤ 5,000,000)과 K (1 ≤ K ≤ N)이 주어진다. 둘째에는 A1, A2, ..., AN이 주어진다. (-109 ≤ Ai ≤ 109)
출) A를 정렬했을 때, 앞에서부터 K번째 있는 수를 출력한다.
풀이 & 코드
솔직히 푼 거 후회했다. 7전 1승의 너덜너덜한 승리를 쥐고, 연구과제로 남기려고 작성한다.
1. 라이브러리 활용
1차 시도 : 시간 초과 ❌
제한 시간 2초, 찾아보니 자바는 (제한시간)*2 +1 초 준다고 한다. 그런데도 초과.
import java.io.*;
import java.util.*;
public class Main{
public static void main(String args[]) throws IOException {
Scanner sc = new Scanner(System.in);
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = sc.nextInt();
int k = sc.nextInt();
int[] arr = new int[n];
for(int i=0; i < n; i++) {
arr[i] = sc.nextInt();
}
Arrays.sort(arr);
bw.write(String.valueOf(arr[k-1]));
sc.close();
bw.flush();
bw.close();
}
}입력받을 때 시간 소모가 많은 탓이라고 생각했다(Scanner).
다른 이유도 있을까하여 질문 게시글을 찾다보니, 세상에 <Quick Sort> 얘기가 나오는 것이다.
알고리즘 시간 때 배운 정렬을 왜 안 써먹었지 충격에 남은 도전은 QuickSort 에 전념하게 된다.
(여기에 너무 집착하였던 게 패인의 요인이었다.)
2. Quick Sort
Quick Sort 복습
pivot, low, high가 있고, pivot 다음 부터 low가 할당되고 n값 있는 쪽이 high 다.
주요 개념에는 Swap과 Cross가 있다.
low와 high가 멈추면(stop), 두 수의 교환이 일어난다(Swap).
- low : pivot보다 더 큰 값을 만나면 stop
- high : pivot보다 더 작은 값을 만나면 stop
- low는 오른쪽으로, high는 왼쪽으로 이동하며 같이 진행한다.
high <= low 되면 pivot값과 바뀐다(Cross).
흑, 슬프게도 개념은 이해가 되었으나 코드로 작성하려니 까마득해졌다.
여러 블로그를 탐방하며 코드를 작성했다.
제출 코드
2~6차 시도 : 시간 초과 또는 틀렸습니다. ❌
import java.io.*;
import java.util.*;
public class Main{
public static int partition(Integer[] arr, int left, int right) {
int mid = (left + right) / 2;
swap(arr, left, mid); //중앙값을 첫 번째 요소(pivot)으로 이동
int pivot = arr[left];
int i = left, j = right;
while(i<j) {
//j는 오른쪽에서 왼쪽으로, pivot보다 작은 수 찾음(Stop).
while(pivot < arr[j]) {
j--;
}
//i는 왼쪽에서 오른쪽으로, pivot보다 큰 수 찾음(Stop).
while(i<j && pivot >= arr[i]) {
i++;
}
swap(arr, i, j); //찾은 i와 j를 교환
}
//arr[i]=arr[j]가 되었을 때 반복문에서 벗어나게 됨(Cross).
//Cross : Pivot과 교환
arr[left] = arr[i];
arr[i] = pivot;
return i;
}
public static void swap(Integer[] arr, int a, int b) {
int temp = arr[b];
arr[b] = arr[a];
arr[a] = temp;
}
public static void quicksort(Integer[] arr, int left, int right, int k) {
if(left < right) {
//partition을 통해 구한 pivot과 k를 비교해 해당 부분집합에 재귀호출을 반복
int pivot = partition(arr, left, right);
if (pivot == k-1) return;
else if (pivot > k-1) quicksort(arr, left, pivot - 1, k);
else quicksort(arr, pivot + 1, right, k);
}
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
Integer[] arr = new Integer[n];
st = new StringTokenizer(br.readLine());
for(int i=0; i<n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
quicksort(arr, 0, n-1, k-1);
System.out.println(arr[k-1]);
br.close();
}
}더할나위 없이 좋은 코드라고 생각했다.
그런데 결과는 <시간 초과, 틀렸습니다.> 제시된 예제와 질문 게시판의 반례와
이 문제를 푼 사람들이 블로그에 적어둔 반례도 다 통과했다. 그런데 왜???
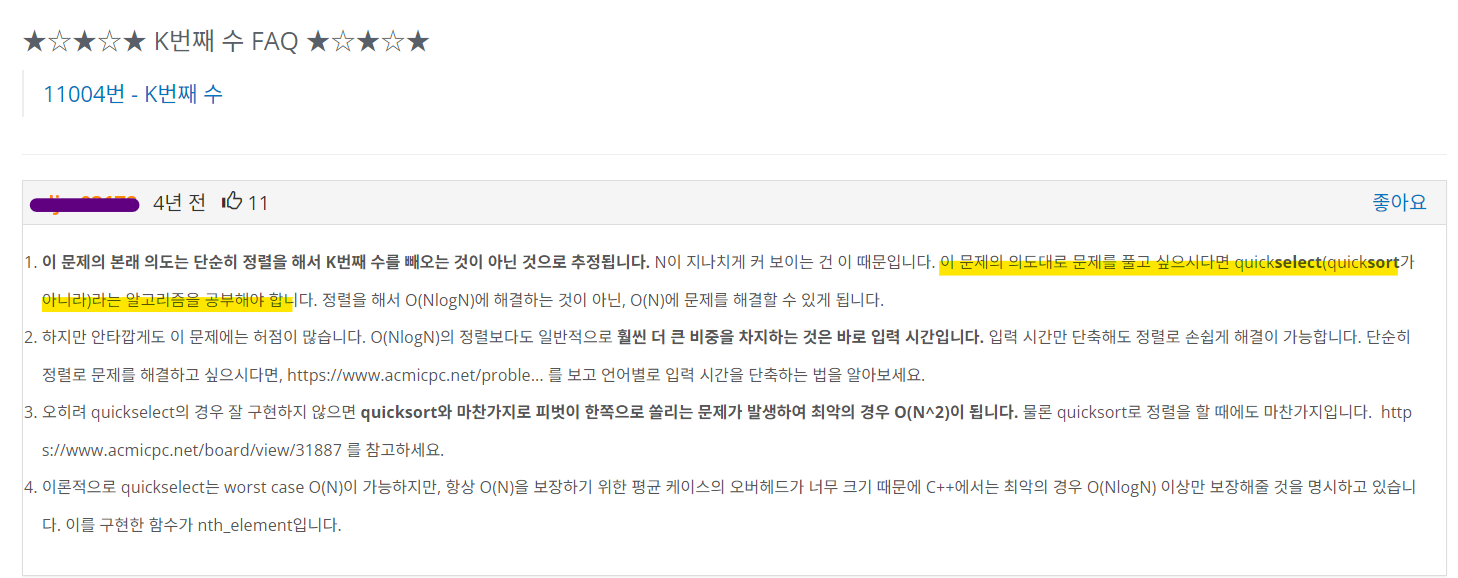
어느 지식인의 FAQ를 보게 되었다. 그렇다. QuickSort로는 풀 수 없고, QuickSelect를 사용해야 한다.
그럼 이전에 통과한 사람들은 뭘까 싶지만,
세월이 흘러... 백준이 업데이트가 되었다고 생각하자... 지금 통과가 안 되는 걸 어떡하나...
악으로 깡으로 찾다보니 int[] 배열보다 WrapperClass인 Integer[]로 했을 때 빠르다는 것도 발견했다.
(위의 코드) 제출하니 틀렸댄다. int[]로 하면 시간 초과.
새롭게 quickSelect를 공부해서 이 문제를 정복하는 건... 힘들 것 같아서 일단 기록 먼저 해둔다.
3. 최종 제출 코드
그래서 어떤 선택을 했나? 다시 원점으로 돌아갔다^^.
입출력 코드만 바꿔서 제출하니 통과다(메모리, 시간 모두 흐음 싶지만 어쨌든 통과).
7차 시도 : 성공 ✅
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
Integer[] arr = new Integer[n];
st = new StringTokenizer(br.readLine());
for (int i=0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(arr);
System.out.println(arr[k-1]);
}
}
이 문제는 여러모로 의미가 있었다(하하^^^^).
1. quickSort로 정녕 풀 수 없는 것인가라는 연구 과제로 남기게 되었고
2. 시간 소요를 위해 int[]보다 Integer[]를 쓰는 것이 더 좋을 때가 있다는 것을 알게 되었다.
3. quickSort가 가지는 최악의 시간 복잡도를 고려하여... 적절한 알고리즘을 선택해야 한다는 깨달음도 얻었다.
그 밖에 System.currentTimeMills(); 을 적극 활용해서 무의미한 제출을 없애야겠다고 생각했다.
[참고] QuickSort 작성할 때 도움이 되었던 블로그
https://log-laboratory.tistory.com/45